Funções

Tradicionalmente, é uma regra que liga um número (argumento) a outro (valor). É usado na ciência para descrever processsos onde uma quantidade afeta outra.

Uma função \( f \) de um conjunto \( X\) em um conjunto \( Y \) é uma relação que associa cada elemento \( x \in X \) a um único elemento \( y \in Y \) que denotamos por \( y = f(x) \). Assim, uma função \( f : X \rightarrow Y \) satisfaz duas condições:

(1) \( D(f) = X \)

(2) \( (x, y) \in f \land (x, z) \in f \implies y = z \)

Aqui \( D(f) \) é dito o domínio da função \( f \) e o conjunto de \( Y \) dado por

\[ f(X) = I(f) = \{f(x): x \in X\} \]

é chamado imagem de \( f \). Designamos o conjunto \( Y \) como o contra-domínio.

Para ser uma função, todo elemento do conjunto \( X \) deve estar associado a outro do conjunto \( Y \), mas a inversa não precisa ser necessariamente verdade.

Exemplo

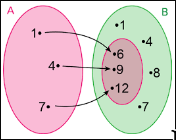
(1) A função \( f : A = \{1, 4, 7\} \rightarrow B = \{1, 2, 6, 7, 8, 9, 12\} \) dada por \( f(x) = x + 5 \) pode ser representada por um diagrama de flechas. Note que \( I(f) = \{6, 9, 12\} \subset B \).

(2) Muitas vezes, funções são dadas sem haver menção ao domínio. Nesse caso, o domínio é entendido como o maior subconjunto de \( \mathbb{R} \) para o qual \( f \) está definida. Por exemplo, para \( f(x) = \frac{\sqrt{x}}{x - 2} \), o domínio de \( f \) é \( [0, \infty) - \{2\} = D(f) \).

Definição

Duas funções \( f : A \rightarrow B \) e \( g : C \rightarrow D \) são iguais se, e somente se, \( A = C, B = D \land \forall x \in A = C, f(x) = g(x) \).

Exemplo

Consideremos as seguintes funções \( f : \mathbb{R} \rightarrow \mathbb{R} \) e \( g : \mathbb{R}_{+} \rightarrow \mathbb{R} \) dadas por \( f(x) = x^{3} \) e \( g(x) = x^{3} \), respectivamente. Então, mesmo tendo expressões iguais, como \( \mathbb{R} \neq \mathbb{R}_{+} \), elas são diferentes.

Combinando funções

Quando o contradomínio das funções são conjuntos em que se podem fazer operações aritméticas, então podemos produzir novas funções a partir de funções dadas combinando-as. Desse modo, se \( A \) é um conjunto qualquer e \(f, g : A \rightarrow \mathbb{R} \), definimos as seguintes novas funções \( f + g \), \( f - g \), \( f \cdot g \) e \( \frac{f}{g} \) de \( A \) em \( \mathbb{R} \) através dos valores de \( f \) e \( g \) em cada \( x \in A \). Isto é

• \( (f + g)(x) = f(x) + g(x) \)
• \( (f - g)(x) = f(x) - g(x) \)
• \( (f \cdot g)(x) = f(x) \cdot g(x) \)
• \( (\frac{f}{g})(x) = \frac{f(x)}{g(x)} (g(x) \neq 0) \)

Exemplo

Seja \( f(x) = x^{2} + 1 \) e \( g(x) = 2x + 1 \), temos as seguintes funções:

• \( (f + g)(x) = x^{2} + 2x + 2 \)
• \( (f - g)(x) = x^{2} - 2x \)
• \( (f \cdot g)(x) = 2x^{3} + x^{2} + 2x + 1\)
• \( (\frac{f}{g})(x) = \frac{(x^{2} + 1)}{(2x + 1)} (x \neq \frac{1}{2}) \)

Restrição

Outra maneira de a partir de uma função \( f : X \rightarrow Y \) se obter uma nova função é restringir a ação da função a um subconjunto de seu domínio ou, ao contrário, estender o domínio.

(1) se \( a \subset X \), a função \( f|_{A} : A \rightarrow Y \) definida por \( f|_{A}(a) = f(a), \forall a \in A \) é dita a restrição de \( f \) ao conjunto \( A \).

(2) se \( X \subset W \) uma função \( g: W \rightarrow B, g(x) = f(x) \forall x \in X \) é dita uma extensão de \( f \).

Exemplo

A função \( f : (0, \infty) \rightarrow \mathbb{R}, f(x) = \frac{1}{x} \) cresce ilimitadamente quando nos aproximamos de \( x = 0 \), porém, sua restrição \( g : [\frac{1}{2}, \infty) \rightarrow \mathbb{R}, g(x) = \frac{1}{x} \) é limitada, com \( g(x) \leq 2, \forall x \in [\frac{1}{2}, \infty) \).

Exemplo

A função raiz quadrada pode ser estendida para todo o conjunto dos reais através da função \( g : \mathbb{R} \rightarrow \mathbb{R}, g(x) = \sqrt{|x|} \).

Composição e funções inversas

Desde que cada função é uma relação e cada relação possui associado a ela sua inversa, isto é, se \( f : A \rightarrow B \) é uma relação, então a relação inversa \( f^{-1} \) é dada por

\[ f^{-1} = \{(y, x) : (x, y) \in f\} \]

diremos que \( f \) é invertível se \( f^{-1} \) é também uma função.

Exemplo

Para a função \( f = \{(x, y) : y = 2x + 1\} \subset \mathbb{R} \times \mathbb{R} \), a inversa de \( f \) é a função

\[ f^{-1} = \{(y, x) : (x, y) \in f\} = \{(y, x) : y = 2x + 1\} = \{(y, x) : x = \frac{y - 1}{2}\} \]

Contudo, para a função \( g = \{(x, y) : y = x^{2}\} \subset \mathbb{R}^{+} \times \mathbb{R}^{+} \), temos que a relação inversa

\[ g^{-1} = \{(y, x) : (x, y) \in g\} = \{(y, x) : y = x^{2}\} = \{(y, x) : x = \pm \sqrt{y}\} \]

não é uma função. De fato, \( (1, 1), (1, -1) \in g^{-1} \) pois \( 1^{2} = (-1)^{2} \). Porém, \( 1 \neq -1 \).

(1) Elementos distintos no domínio \( A \) devem estar associados a elementos distintos no contradomínio \( B \), ou seja, se \( x \neq y \in A \), então \( f(x) \neq f(y) \in B \). Funções que satisfazm esta propriedade são chamadas de funções injetivas.

(2) Cada elemento no contradomínio \( B \) deve ser imagem sob \( f \) de pelo menos um elemento de \( A \). Em outras palavras \( \forall y \in B, \exists x \in A, f(x) = y \), ou ainda, \( I(f) = B \). Funções que satisfazem esta propriedade são ditas funções sobrejetivas.

Desse modo, se a função \( f \) não for bijetiva: injetiva e sobrejetiva, ela não é invertível. Noutras palavras, se \( f \) é invertível, necessariamente ela é bijetiva.

Exemplo

Seja \( f : \mathbb{R} \times \mathbb{R} \rightarrow \mathbb{R} \times \mathbb{R} \) definida por \( f(x, y) = (-x + y, x + y) \). Se \( (x, y), (z, t) \in \mathbb{R} \times \mathbb{R} \) são tais que \( f(x, y) = f(z, t) \), então

\[ (-x + y, x + y) = (-z + t, z + t) \]

Isto implica que

\[ -x + y = -z + t \implies x + y = z + t \]

Somando esssas identidades, obtemos que \( y = t \) e, consequentemente, \( x = z \). Assim, \( (x, y) = (z, t) \) e a função \( f \) é injetiva. Agora, para verificarmos se a função \( f \) é sobrejetiva, tomemos um elemento genérico \( (c, d) \) em \( \mathbb{R} \times \mathbb{R} \) e busquemos um elemento no domínio \( (x, y) \in \mathbb{R} \times \mathbb{R}, f(x, y) = (c, d) \). Por definição de \( f \), temos que \( (-x + y, x + y) = (c, d) \), donde \( -x + y = c \land x + y = d \). Somando essas equações obtemos que \( y = \frac{c + d}{2} \). Substitutindo em uma das equações acima, concluímos que \( x = \frac{d - c}{2} \). Portanto,

\[ f\left(\frac{c + d}{2}, \frac{d - c}{2}\right) = (c, d) \]

e a função \( f \) é sobrejetiva. Desse modo, \( f \) é uma função bijetiva.

Composição

Seja \( f : A \rightarrow B \) e \( g : B \rightarrow C \). A composição de \( g \) e \( f \) é a relação

\[ g \circ f = \{(x, y) : \forall y \in B, (x, y) \in f \land (y, z) \in g\} = \{(x, z) : \exists y \in B, f(x) = y \land g(y) = z\} = \{(x, z) : g(f(x)) = z\} \]

Logo, \( g \circ f : A \rightarrow C \) será definida por \( (g \circ f)(x) = g(f(x)) \).

Exemplo

Seja \( f(x) = sen(x) \) e \( g(x) = x^{2} + 6x \).

\[ (f \circ g)(x) = f(g(x)) = sen(g(x)) = sen(x^{2} + 6x) \]

e

\[ (g \circ f)(x) = g(f(x)) = sen^{2}(x) + 6sen(x) \]

Como a operação de composição de funções não é comutativa, \( f \circ g \) pode ser diferente de \( g \circ f \).

Observação Como a composição de relações é associativa e funções são relações, a composição de funções também é associativa, ou seja, \( f : A \rightarrow B, g : B \rightarrow C \land h : C \rightarrow \implies (h \circ f) \circ g = h \circ (f \circ g) \).

Definição

Se uma função \( f : A \rightarrow B \) é bijetiva, então ela é invertível.