Relações

Definição

Sejam \( A \) e \( B \) conjuntos. Uma relação \( R \) entre \( A \) e \( B \) é um subconjunto de \( A \times B \). Assim, se \( (a, b) \in R \), escrevemos \( aRb \) (ou \( a ~ b \)) par aexpressar que \( a \) e \( b \) estão relacionados. O domínio de uma relação é o conjunto \( D(r) = \{x \in A : \exists y \in B \text{ tal que } xRy\} \) e a imagem da relação é o conjunto \( I(R) = \{y \in B : \exists x \in A \text{ tal que } xRy\} \).

Exemplo

Seja \( A = \{1, 2, 3\} \) e \( B = \{2, 3, 4\} \). Defina a relação \( R = \{(x, y) : x + 1 < y\} \).

Resolução

O domínio fica na esquerda e a imagem na direita.

Exemplo

(1) Sobre \( \mathbb{Z} \) consideremos a relação \( R = \{(x, y) \in \mathbb{Z} \times \mathbb{Z} : x + y = 0\} \). Enstão \( R = \{..., (-1, 1), (1, -1), (0, 0), (2, -2), ...\} \) é o conjunto de pontos sobre a reta dada pela equação \( y = -x \) com coordenadas inteiras.

(2) Sobre o conjunto \( \mathbb{N} \times \mathbb{N} \) considere a relação \( (m, n)R(s, r) \iff m + r = n + s \). Esta relação possui uma infinidade de elementos. Por exemplo, \( (1, 1)R(2, 2), (1, 3)R(5, 7), ...\).

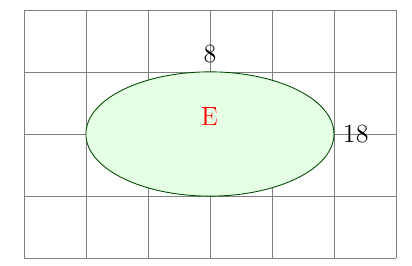
(3) Seja \( E = \{(x, y) \in \mathbb{R} \times \mathbb{R} : \frac{x^{2}}{324} + \frac{y^{2}}{64} \leq 1\} \). O gráfico de \( E \) é constituído pelos pontos do plano que estão dentro e sobre a elipse.

(4, 5) Relações também podem ser representadas usando grafos e fluxogramas.

Definição

SE \( R \) é uma relação entre os conjuntos \( A \) e \( B \), então definimos a inversa de \( R \), denotada por \( R^{-1} \), como sendo a relação

\[ R^{-1} = \{(x, y) \in B \times A : (x, y) \in R\} \]

Exemplo

(1) No caso da relação \( R = \{(x, y) : x + 1 < y\} \) em \( A \times B \), sua inversa é dada pela relação \( R^{-1} = \{(3, 1), (4, 1), (4, 2)\} \) em \( B \times A \). Ou seja, os papéis de \( x \) e \( y \) foram trocados; enquanto em \( R \) o critério era que o segundo componente do par ordenado fosse maior que o primeiro mais uma unidade, em \( R^{-1} \) o primeiro componente é que é maior que o segundo mais uma unidade.

(2) Seja \( R \) uma relação sobre o conjunto dos números reais \( \mathbb{R} \) definida por \( xRy \iff y = x^{2} \). Determine \( R^{-1} \).

Definição

Seja \( R \) uma relação entre os conjuntos \( A \) e \( B \) e seja \( S \) uma relação entre os conjuntos \( B \) e \( C \). A composição de \( R \) e \( S \) é definida como sendo o subconjunto de \( A \times C \) dado por

\[ S \circ R = \{(a, c) \in A \times C : \exists{b} \in B \text{ tal que } (a, b) \in R \text{ e } (b, c) \in S\} \]

O domínio de \( S \circ R \) será um subconjunto do domínio da relação \( R \) e a imagem estará contida na imagem da relação \( S \). E para um elemento pertencer a composição é necessário que haja um elemento em \( B \) fazendo a conexão entre elementos de \( A \) e \( C \).

Exemplo

Consideremos os conjuntos \( A = \{1, 2, 3, 4\} \), \( B = \{p, q, r, s\} \) e \( C = \{x, y, z\} \). Seja \( R = \{(1, p), (1, q), (2, q), (3, r), (4, s)\} \) uma relação entre \( A \) e \( B \), e tomemos a relação entre \( B \) e \( C \) dada por \( S = \{(p, x), (q, x), (q, y), (s, z)\} \). Então

\[ S \circ R = \{(1, x), (1, y), (2, x), (2, y), (4, z)\}, \]

com \( D(S \circ R) = \{1, 2, 4\} \subset D(R)\) e \( I(S \circ R) = \{x, y, z\} \subset I(S) \).

Exemplo

Se \( R \) é uma relação entre \( A \) e \( B \) e \( S \) é uma relação entre \( B \) e \( A \), então nem sempre é verdade que \( S \circ R = R \circ S \). Por exemplo, tome sobre \( \mathbb{R} \times \mathbb{R} \) as seguintes relações

\[ R = \{(x, y) \in \mathbb{R} \times \mathbb{R} : y = x + 1\} \text{ e } S = \{(y, z) \in \mathbb{R} \times \mathbb{R} : z = y^{2}\} \]

Então

\[ R \circ S = \{(y, x) \in \mathbb{R} \times \mathbb{R} : x = y^{2} + 1\} \]

E

\[ S \circ R = \{(y, x) \in \mathbb{R} \times \mathbb{R} : x = (y + 1)^{2}\} \]

Observamos agora que a composição de uma relação \( R \) com sua inversa \( R^{-1} \) nem sempre é a relação identidade (que associa um objeto a ele mesmo).

Teorema

Suponha \( A \), \( B \), \( C \) e \( D \) conjuntos. Sejam \( R \) uma relação entre \( A \) e \( B \), \( S \) uma relação entre \( B \) e \( C \), e \( T \) uma relação entre \( C \) e \( D \). Então, considerando que sejam válidas as composições,

(i) \( (R^{-1})^{-1} = R \) (ii) \( T \circ (S \circ R) = (T \circ S) \circ R \) (iii) \( (S \circ R)^{-1} = R^{-1} \circ S^{-1} \)

Relações de Equivalência

Uma relação \( R \) sobre um conjunto \( X \) é chamada relação de equivalência se as seguintes propriedades forem satisfeitas:

(1) Reflexiva: \( \forall x \in X, xRx \)

(2) Simétrica: \( \forall x, y \in X, xRy \implies yRx \)

(3) Transitiva: \( \forall x, y, z \in X, xRy \land yRz \implies xRz \)

Exemplo

Seja \( n \) um inteiro positivo fixado. Então definimos sobre \( \mathbb{Z} \) a seguinte relação: \( aRb \iff a - b = kn, k \in \mathbb{Z} \). Esta relação é chamada congruência módulo \( n \). Ao invés de escrever \( aRb \), costuma-se denotar esta relação por \( a \equiv b \pmod{n}} \). Verifiquemos que esta é uma relação de equivalência.

(1) Vale a reflexividade pois \( a \equiv a \pmod{n} \forall a \in \mathbb{Z} \) uma vez que \( a - a = 0n \)

(2) Vale a simetria pois se \( a \equiv b \pmod{n} \), então

\[ b - a = -(a - b) = -(kn) = (-k)n, \]

o que implica, por definição da relação, que \( b \equiv a \pmod{n} \)

(3) Vale a transitividade pois, \( \forall a, b, c \in \mathbb{Z}, a \equiv b \pmod{n} \land b \equiv c \pmod{n}, \exists k_{1}, k_{2} \in \mathbb{Z} \) satisfazendo \( a - b = k_{1}n \land b - c = k_{2}n \). Assim,

\[ a - c = (a - b) + (b - c) = (k_{1} + k_{2})n \]

e isto implica que \( a \equiv c \pmod{n} \)

Exemplo

Definimos uma relação sobre \( \mathbb{Z} \) por: \( xRy \iff x + 3y = 2k, k \in \mathbb{Z} \). Verifiquemos que esta é uma relação de equivalência.

(1) Vale a reflexividade pois \( \forall x \in \mathbb{Z} \) temos que \( x + 3x = 4x = 2k, k \in \mathbb{Z} \).

(2) Vale a simetria pois se \( xRy \), então \( x + 3y = 2k, k \in \mathbb{Z} \). Consequentemente,

\[ y + 3x = y + 2y - 2y + x + 2x = x + 3y + 2(x - y) = 2(k + x - y) \]

nos diz que \( y + 3x \) é par. Ou seja, \( yRx \).

(3) Vale a transitividade pois, \( \forall x, y, z \in \mathbb{Z}, xRy \land yRz \), temos que \( \exists k_{1}, k_{2} \in \mathbb{Z} \) satisfazendo \( x + 3y = 2k_{1} \) e \( y + 3z = 2k_{2} \). Assim,

\[ x + 3z = x + 3y - 3y + y - y + 3z = (x + 3y) + (y + 3y) + (y + 3z) - 4y = 2(k_{1} + k_{2} - y) \]

é par, e isto implica que \( xRz \) como queríamos mostrar.

Exemplo

Definimos agora a relação sobre \( R \) por: \( xRy \iff |x - y| \leq 1 \). Verifiquemos que esta não é uma relação de equivalência.

(1) Vale a reflexividade pois \( \forall x \in \mathbb{R}, |x - x| = 0 \leq 1\)

(2) Vale a simetria pois \( xRy \implies |x - y| \leq 1 \) e como \( |y - x| = |x - y| \) temos que \( yRx \)

(3) Não vale a propriedade transitiva pois, \( 5R4 \) e \( 4R3 \) porém \( |5 - 3| = 2 > 1 \)

Definição

Uma vez que temos uma relação de equivalência \( R \) sobre um conjunto \( X \), definimos a classe de equivalência de um elemento \( x \in X \), denotada por \( [x] \), como sendo o subconjunto de todos os elementos em \( X \) que estão relacionados a \( x \), isto é,

\[ [x] = \{y \in X : yRx\} \]

O conjunto de todas as classes é chamado conjunto quociente e denotado por

\[ X/R = \{[x] : x \in X\} \]

Exemplo

No caso da relação de equivalência \( x \equiv y \pmod{3} \) sobre \( \mathbb{Z} \), temos que

\[ [x] = \{x \in \mathbb{Z} : y \equiv x \pmod{3}\} & = \{y \in \mathbb{Z} : y = 3k + x, k \in \mathbb{Z}\} & = \{3k + x : x \in \mathbb{Z}\} \]

Assim, a classe de equivalência do elemento \( \ \in \mathbb{Z} \) é constituída pelos inteiros que ao serem divididos por 3 deixam resto \( x \). Logo, há somente três classes distintas:

\[ [0] = \{0, \pm 3, \pm 6, ...\} [1] = \{1,4, -2,7, -5 ...\} [2] = \{2,5, -1,8, -4, ...\} \]

correspondentes aos elementos que deixam restos 0, 1 ou 2, respectivamente. Portanto,

\[ Z/R = \{[0], [1], [2]\} \]

Exemplo

A relação \( R \) definida sobre o conjunto dos números reais \( R \) por \( xRy \iff x^{2} = y^{2} \) é uma relação de equivalência. As classes de equivalência têm a forma

\[ [x] = \{y \in \mathbb{R} : yRx\} = \{y \in : y^{2} = x^{2}\} = \{-x, x\} \]

Logo, \( \mathbb{R}/R \) possui infinitas classes de equivalência. Assim, temos as classes \( [\pi] = \{-\pi, \pi\} \) e \( [\sqrt{2} = \{-\sqrt{2}, \sqrt{2}\} \).

Sobre o conjunto quociente \( X/R \) podemos definir uma operação de adição e uma operação de multiplicação da seguinte forma:

\[ [x] + [y] = [x + y] \]

e

\[ [x] \cdot [y] = [xy] \]

Com estas operações podemos construir o conjunto dos inteiros a partir dos números naturais da seguinte forma: defina a relação de equivalência \ ( R \) sobre \( \mathbb{N} \times \mathbb{N} \) por \( (a, b)R(c, d) \iff a + b = b + c \).

Definição

Seja \( X \) um conjunt não-vazio e seja \( I \) um conjunto de índices. Uma partição é uma relação de subconjuntos \( \{A_{\alpha}_{\alpha \in I} \in X \) tal que:

(1) \( \forall \alpha \in I, A_{\alpha} \neq \varnothing \)

(2) \( X = \bigcup_{\alpha \in I} A_{\alpha} \)

(3) \( \forall \alpha, \beta \in I, A_{\alpha} \cap A_{\beta} \implies A_{\alpha} = A_{\beta} \)

Exemplo

A família de intervalos \( A_{n} = [n, n + 1) \), com \( n \in \mathbb{Z} \), particiona o conjunto \( \mathbb{R} \). De fato, cada \( A_{n} \neq \varnothing, \mathbb{R} = \bigcup_{n \in \mathbb{Z}} A_{n} \) e se \( A_{n} \cap A_{m} \neq \varnothing, como os intervalos \( [n, n + 1) \) e \( [m, m + 1) \) são ou iguais ou disjuntos, segue que \( A_{n} = A_{m} \).

Teorema

seja \( \{A_{\alpha}\}{\alpha \in I} \) uma pratição do conjunto \( X \). Para \( x, y \in X \) define \( xRy \iff \exists A{\alpha}, x, y \in A \). Então \( R \) é uma relação de equivalência sobre \( X \) e \( X/R = \{A_{alpha} : \alpha \in I\} \).

Relação de Ordem

Relação que compara os elementos de um conjunto e os classifica de alguma forma. Requer que a propriedade transitiva seja válida, mas não a simétrica.

Definição

Uma relação \( R \) sobre um conjunto \( X \) é dita uma relação de ordem parcial se ela é reflexiva, antissimétrica e transitiva, onde anti-simetria significa que \( \forall x, y \in X, xRy \land yRx \) temos que \( x = y \). O conjunto \( X \) é dito parcialmente ordenado.

Exemplo

A ordem padrão \( \leq \) (menor ou igual) sobre \( \mathbb{R} \) é claramente uma relação de ordem parcial sobre \( \mathbb{R} \).

Exemplo

Para o conjunto dos números naturais \( \mathbb{N} \), a relação \( R \) é definida por \( aRb \iff a|b \) é uma relação de ordem. Com efeito, a propriedade reflexiva é válida, pois \( \forall n \in \mathbb{N}, n = n \cdot 1, n|n \). A relação \( R \) também é anti-simétrica, pois \( aRb \land bRa \implies \exists m, n \in \mathbb{N}, b = am \land a = bn \). Assim, \( a = (am)n = a(mn) \). Mas isto somente é possível se \( mn = 1 \), donde concluímos que \( m = n = 1 \). Portanto, \( a = b \). Por fim, verificamos que a propriedade transitiva também é válida. \( aRb \land bRc \implies \exists m, n \in \mathbb{N}, b = am \land c = bn \). Assim, \( c = (am)n = a(mn) = ak \). Portanto, \( a \) divide \( c \) e isto implica que \( aRc \).

Exemplo

Consideremos um conjunto \( X \) e sobre seu conjunto potência \( \mathcal{P}(X) \) a relação definida por \( A \preceq B \iff A \subset B \). Uma vez que \( A \subset A \) segue que \( A \preceq A \) ( \( A \) precede ou é igual a \( A \) ) e a relação é reflexiva. Quando estudamos Conjuntos vimos que \( A \subset B \land B \subset C \implies A \subset C \). Isto é \( A \preceq B \land B \preceq C \implies A \preceq C \) e a relação é transitiva. Também do capítulo sobre conjuntos vimos que \( A \subset B \land B \subset C \implies A = B \). Logo, \( a \preceq B \land B \preceq A \implies A = B \), de modo que vale a propriedade antissimétrica. Portanto, o conjunto ( \( \mathcal{P}(X), \subset \) ) é parcialmente ordenado.

Ordem lexicográfica

Seja \( A \) um conjunto e seja \( \preceq \) uma ordem parcial sobre \( A \). Dizemos que \( (a_{1}, a_{2})R(x_{1}, x_{2}) \iff a_{1} \preceq x_{1} \lor a_{1} = x_{1} \land a_{2} \preceq x_{2} \). Mostremos que \( R \) é uma relação de ordem parcial. A propriedade reflexiva é válida, uma vez que \( \forall (x,y) \in A \) temos que \( x = x \land y \preceq y \). Logo, \( (x,y)R(x, y) \). Para verificarmos a antissimetria, suponha que \( (x_{1}, y_{2})R(x_{2}, y_{2}) \) e \( (x_{2}, y_{2})R(x_{1}, y_{1}) \). Assim, do fato que \( x_{1] \preceq x_{2} \land x_{2} \preceq x_{1} \) segue que \( x_{1} = x_{2} \) e, consequentemente, \( y_{1} \preceq y_{2} \land y_{2} \preceq y_{1} \). Portanto, \( y_{1} = y_{2} \land (x_{1}, y_{1}) = (x_{2}, y_{2}) \). Por fim, para mostrarmos a validade da propriedade transitiva, suponha que \( (x_{1}, y_{1})R(x_{2}, y_{2}) \land (x_{2}, y_{2})R(x_{3}, y_{3}) \). Temos quatro casos a considerar:

(a) se \( x_{1} \preceq x_{2} \land x_{2} \preceq x_{3} \), então, pela transitividade de \( \preceq \) temos que \( x_{1} \preceq x_{3} \). Logo, \( (x_{1}, y_{1})R(x_{3}, y_{3] \)

(b) se \( x_{1} \preceq x_{2} \land x_{2} = x_{3} \), então, \( x_{1} \preceq x_{3} \land (x_{1}, y_{1})R(x_{3}, y_{3} \)

(c) se \( x_{1} = x_{2} \land x_{2} \preceq x_{3} \), então, \( x_{1} \preceq x_{3} \land (x_{1}, y_{1})R(x_{3}, y_{3} \)

(d) se \( x_{1} = x_{2} \land x_{2} = x_{3} \), então, \( x_{1} = x_{3} \), e, desse modo, \( y_{1} \preceq y_{2} \land y_{2} \preceq y_{3} \implies y_{1} \preceq y_{3} \) \( \therefore (x_{1}, y_{1})R(x_{3}, y_{3} \)

O termo "parcial" numa relação de ordem parcial refere-se ao fato que existem elementos no conjunto que não são comparáveis. Por exemplo, no conjunto \( \mathbb{N} \) com a relação de divisibilidade os elementos 2 e 3 não estão relacionados (nem 2 divide 3, nem 3 divide 2).