Noções de Lógica
Cálculo Proposicional
Na maioria das ciências, o raciocínio utilizado é indutivo, isto é, aquele baseado na experiência e experimentação. Na matemática, esse tipo de raciocínio também chega a ser usado, mas nem sempre é confiável.
Nesse campo, o mais usado é o dedutivo. Se as premissas (hipóteses) são verdadeiras e as leis aplicadas estão corretas, então a conclusão é necessariamente verdadeira.
Proposição
Uma proposição é uma afirmação que é verdadeira ou falsa, mas não ambas. Chamamos este fato de princípio do meio excluído.
Exemplo
Consideremos as seguintes afirmações:
(1) \( \sqrt{2} \) é um número irracional.
(2) Todo triângulo é isósceles.
(3) Que horas são?
(4) \( x + 1 = 2 \).
(5) Existem infinitos números primos.
(6) Vixe Maria!
(7) Esta afirmação é falsa.
(8) Paulo é um bom professor.
Questões imperativas e exclamativas não são proposições, como em (3) e (6). A afirmação (4) pode ser verdadeira ou falsa, dependendo do valor de \( x \) associado. Ela é um predicado, uma afirmação contendo uma ou mais variáveis que se torna uma proposição quando atribuímos valores às variáveis. Por exemplo, chamando esse predicado de \( A(x) \) e fazendo \( A(1) \), temos que a proposição é verdadeira (o que não é o caso para \( A(2) \), ou qualquer valor de \( x \) na verdade).
A afirmação (7) é um paradoxo. A afirmação (8) não pode ser considerada uma proposição, pois é apenas uma opinião.
(1), (2) e (5) são proposições.
No estudo de lógica, usamos letras maiúsculas para representar proposições simples (geralmente \( P \), \( Q \), \( R \) e \( S \)), e atribuímos o valor \( V \) ou \( F \) a uma proposição se ela for verdadeira ou falsa, respectivamente. Usamos dos chamados conectivos lógicos para formar novas proposições a partir de outras existentes.
| Conectivo | Símbolo |
|---|---|
| e (conjunção) | \( \land \) |
| ou (disjunção) | \( \lor \) |
| não (negação) | \( ~ \) ou \( \neg \) |
Conjunção
Numa conjunção, sendo \( P \) e \( Q \) proposições, então \( P \land Q \) é uma afirmação verdadeira quando ambos, \( P \) e \( Q \), são verdadeiros, e falsa caso contrário.
Esta afirmação é usualmente apresentada na forma de uma tabela-verdade, na qual se verifica o valor lógico de uma afirmação composta a partir das combinações dos valores lógicos das sentenças individuais que ela contém. O número de possibilidades para uma proposição como esta é de \( 2^{n} \), sendo \( n \) o número de proposições.
A estratégia para construir uma tabela-verdade com esse tipo de preposição é de sugerir que a proposição inicial é verdadeira na primeira metade dos casos e falsa no resto. Onde a primeira é verdadeira, em metade dos casos a segunda é verdadeira e na outra metade falsa; onde a primeira é falsa, a segunda é verdadeira em metade dos casos e falsa na outra metade.
Podemos fazer isso com quantas proposições quisermos.
Aqui temos um exemplo com duas:
| \( P \) | \( Q \) | \( P \land Q \) |
|---|---|---|
| \( V \) | \( V \) | \( V \) |
| \( V \) | \( F \) | \( F \) |
| \( F \) | \( V \) | \( F \) |
| \( F \) | \( F \) | \( F \) |
E outro com três:
| \( P \) | \( Q \) | \( R \) | \( P \land Q \land R \) |
|---|---|---|---|
| \( V \) | \( V \) | \( V \) | \( V \) |
| \( V \) | \( V \) | \( F \) | \( F \) |
| \( V \) | \( F \) | \( V \) | \( F \) |
| \( V \) | \( F \) | \( F \) | \( F \) |
| \( F \) | \( V \) | \( V \) | \( F \) |
| \( F \) | \( V \) | \( F \) | \( F \) |
| \( F \) | \( F \) | \( V \) | \( F \) |
| \( F \) | \( F \) | \( F \) | \( F \) |
Disjunção
Numa disjunção, sendo \( P \) e \( Q \) proposições, então \( P \lor Q \) é uma afirmação verdadeira quando pelo menos um ds componentes for verdadeiro, e falso quando ambas forem falsas.
Aqui temos um exemplo com duas:
| \( P \) | \( Q \) | \( P \lor Q \) |
|---|---|---|
| \( V \) | \( V \) | \( V \) |
| \( V \) | \( F \) | \( V \) |
| \( F \) | \( V \) | \( V \) |
| \( F \) | \( F \) | \( F \) |
E outro com três:
| \( P \) | \( Q \) | \( R \) | \( P \land Q \land R \) |
|---|---|---|---|
| \( V \) | \( V \) | \( V \) | \( V \) |
| \( V \) | \( V \) | \( F \) | \( V \) |
| \( V \) | \( F \) | \( V \) | \( V \) |
| \( V \) | \( F \) | \( F \) | \( V \) |
| \( F \) | \( V \) | \( V \) | \( V \) |
| \( F \) | \( V \) | \( F \) | \( V \) |
| \( F \) | \( F \) | \( V \) | \( V \) |
| \( F \) | \( F \) | \( F \) | \( F \) |
Uma disjunção pode ser exclusiva ("ou um ou outro, nunca ambos", denotado por \( \oplus \) ou \( \underline{\lor} \)) ou inclusiva.
Negação
Na matemática, a dupla negação de uma proposição resulta na negação da negação, resultando nela mesma.
Exemplo
- \( P \): "Gosto de sorvete"
- \( ~P \): "Não gosto de sorvete"
- \( ~(~P) \): "Gosto de sorvete"
| \( P \) | \( ~P \) |
|---|---|
| \( V \) | \( F \) |
| \( F \) | \( V \) |
Observação A negação somente inverte o valor lógico de uma proposição, ou seja, não é só porque que uma proposição esteja sendo negada que ela é falsa. Ela pode ser falsa por padrão (fazendo com que sua negação seja verdadeira).
Implicações
Uma implicação \( P \implies Q \) é falsa somente quando a hipótese \( P \) é verdadeira e a conclusão \( Q \) é falsa. Um modo de entender o valor verdade de uma afirmação condicional é pensar nela como uma obrigação, uma promessa ou um contrato.
| \( P \) | \( Q \) | \( P \implies Q \) |
|---|---|---|
| \( V \) | \( V \) | \( V \) |
| \( V \) | \( F \) | \( F \) |
| \( F \) | \( V \) | \( V \) |
| \( F \) | \( F \) | \( V \) |
Em uma implicação \( P \implies Q \), \( P \) é chamada de hipótese e \( Q \) de conclusão (ou tese).
Exemplo
(1) Se o número \( a \) divide \( b \) e, por usa vez, \( b \) divide \( c \), então \( a \) divide \( c \).
(2) Se \( x \neq 0 \), então \( x^{2} > 0 \).
(3) Se \( p \) é primo e \( p > 2 \), então \( p \) é impar.
Equivalência Lógica
Duas afirmações \( P \) e \( Q \), simples ou compostas, são logicamente equivalentes se possuem a mesma tabela-verdade, ou seja, se possuem os mesmos valores lógicos. Denotamos este fato por \( P \equiv Q \).
Exemplos de Equivalência
- \( ~(P \lor Q) \equiv ~P \land ~Q \)
- \( ~(P \land Q) \equiv ~P \or ~Q \)
- \( (P \implies Q) \equiv (~P \lor Q) \)
Inversa
\[ ~P \implies ~Q \]
Assim como a negação, o sinal não importa, e sim o conteúdo.
Exemplo
(1) "Se eu sou sergipano, então eu sou brasileiro p" é um implicação válida, porém sua inversa é falsa: "Se eu não sou sergipano, então eu não sou brasileiro".
(2) "Se \( x \) é par, então x^{2} é par" é uma implicação verdadeira que possui uma inversa também vedadeira? "Se x é ímpar, então x^{2} é ímpar".
Contrapositiva
\[ ~Q \implies ~P \]
Recíproca
\[ Q \implies P \]
Se, e somente se
Quando em uma implicação \( P \implies Q \) é verdadeira e sua recíproca \( Q \implies P \) também é verdadeirqa, dizemos que temos uma bi-implicação (ou bicondicional), denotada por \( P \iff Q \) (tê-se \( P \) se, e somente se, \( Q \)).
| \( P \) | \( Q \) | \( P \iff Q \) |
|---|---|---|
| \( V \) | \( V \) | \( V \) |
| \( V \) | \( F \) | \( F \) |
| \( F \) | \( V \) | \( F \) |
| \( F \) | \( F \) | \( V \) |
Tautologias e Contradições
Uma tautologia é uma afirmação sempre verdadeira.
| \( P \) | \( Q \) | \( P \lor Q \) | \( P \implies (P \lor Q) \) |
|---|---|---|---|
| \( V \) | \( V \) | \( V \) | \( V \) |
| \( V \) | \( F \) | \( V \) | \( V \) |
| \( F \) | \( V \) | \( V \) | \( V \) |
| \( F \) | \( F \) | \( F \) | \( V \) |
Uma contradição é uma afirmação sempre falsa.
| \( P \) | \( Q \) | \( ~P \) | \( ~Q \) | \( ~P \land Q \) | \( P \lor ~Q \) | \( (~P \land Q) \land (P \lor ~Q) \) |
|---|---|---|---|---|---|---|
| \( V \) | \( V \) | \( F \) | \( F \) | \( F \) | \( V \) | \( F \) |
| \( V \) | \( F \) | \( F \) | \( V \) | \( F \) | \( V \) | \( F \) |
| \( F \) | \( V \) | \( V \) | \( F \) | \( V \) | \( F \) | \( F \) |
| \( F \) | \( F \) | \( V \) | \( V \) | \( F \) | \( V \) | \( F \) |
Observação Expressões lógicas regulares são chamadas de contingências.
Formas Normais Disjuntiva e Conjuntiva
A Forma Normal Disjuntiva permite encontrar uma função lógica indeterminada mediante uma conjunção de disjunções, enquanto a conjuntiva usa uma disjunção de conjunções.
Exemplo
Qual a sentença lógica que fornecea tabela-verdade abaixo?
| \( P \) | \( Q \) | \( R \) | Função Lógica |
|---|---|---|---|
| \( V \) | \( V \) | \( V \) | \( V \) |
| \( V \) | \( V \) | \( F \) | \( V \) |
| \( V \) | \( F \) | \( V \) | \( F \) |
| \( V \) | \( F \) | \( F \) | \( V \) |
| \( F \) | \( V \) | \( V \) | \( F \) |
| \( F \) | \( V \) | \( F \) | \( V \) |
| \( F \) | \( F \) | \( V \) | \( V \) |
| \( F \) | \( F \) | \( F \) | \( F \) |
Para encontrar o FND, olhamos para as linhas em que o resultado da função lógica é verdadeiro (1, 2, 4, 6 e 7). Então criamos fórmulas que fornece um resultado verdadeiro através de conjunções:
\[ FND: (P \land Q \land R) \lor (P \land Q \land ~R) \lor (P \land ~Q \land ~R) \lor (~P \land Q \land ~R) \lor (~P \land ~Q \land R) \]
Por outro lado, para o FNC, olhamos as linhas em uqe o resultado é falso (3, 5 e8 ); e tomamos disjunções de forma que forneça este resultado:
\[ FNC: (~P \lor Q \lor ~R) \land (P \lor ~Q \lor ~R) \land (~P \lor ~Q \lor ~R) \]
Quantificadores
Uma sentença aberta (ou predicado) é uma sentença contendo uma ou mais variáveis, que, ao serem substituídas por valores, viram proposições. O universo de discurso é o conjunto dos valores válidos das variáveis.
Exemplo
- \( x > 3 \) é uma sentença aberta
- \( 2 > 3 \) é uma proposição falsa, derivada da sentença aberta
Quantificador Universal
Para uma sentença aberta \( P(x) \) com variável \( x \) num universo de discurso \( \mathbb{U} \), a sentença \( \forall x \in \mathbb{U}, P(x) \) (lida: para todo x em U, P(x)) é verdadeira precisamente quando \( P(x) \) é verdadeiro qualquer que seja \( x \) em \( \mathbb{U} \). O símbolo \( \forall \) é chamado de quantificador universal.
Quantificador Existencial
A sentença \( \exists x \in \mathbb{U}, P(x) \) (lida: existe x em U tal que P(x)) é verdadeira quando existe pelo menos um \( x \) no universo de discurso \( \mathbb{U} \) tal que \( P(x) \) é verdadeiro. O símbolo \( \exists \) chamado de quantificador existencial. Quando o objeto é único, denotamos este fato pelo símbolo \( \exists ! \).
Exemplo
(1) \( \forall x \in \mathbb{R}, x^{2} \geq 0 \).
(2) \( \forall x, y \in \mathbb{Q} \) (o produto \( xy \) e a soma \( x + y \) são racionais).
(3) \( \forall x \in \mathbb{R}, (x \geq 3 \implies x^{2} \geq 9) \).
(4) \( \exists x \in \mathbb{Z}, x^{2} = 4 \).
(5) Existem dois números primos tal que sua soma é um número primo.
(6) Para cada número primo \( x \) menor que 10, \( x^{2} + 4 \) é primo.
(7) Existe alguém que não entendeu a definição de quantificador existencial.
Negação
A negação de um quantificador universal resulta num existencial e vice-versa.
Exemplo
"Todos serão reprovados em Fundamentos de Matemática \( (\forall x \in \mathbb{U}, P(x)) \) ⇝ "Existe uma pessoa que não será reprovada em Fundamentos de Matemática" \( (\exists x \in \mathbb{U}, ~P(x)) \)
Validade de Argumentos
Um arugmento com hipóteses \( P_{1} \), \( P_{2} \), ..., \( P_{n} \) e conclusão \( Q \) é dito ser válido. se sempre que \( P_{1} \), \( P_{2} \), ..., \( P_{n} \) forem verdadeiros, então \( Q \) também o for. Denotaremos um argumento por
\[ P_{1}, P_{2}, ..., P_{n} \vdash Q \]
Assim,
\[ (P_{1} \land P_{2} \land ... \land P_{n}) \implies Q \]
é uma tautologia. Caso contrário, dizemos que o argumento é inválido.
Tabela-Verdade
Nela, consideramos todas as possibilidades.
Exemplo
Verificar mediante tabela-verdade a validade do argumento seguinte: "Se Carlos está com fome, então, ele come. Carlos dorme ou não come. Carlos está acordado. Portanto, Carlos não está com fome."
O primeiro passo consiste na representação do argumento na forma simbólica, em termo de proposições simples. Chamando as proposições simples "...fome", "...come" e "..acordado" de \( P \), \( Q \) e \( R \), respectivamente, o argumento pode ser escrito na linguagem da lógica proposicional como
\[ P \implies Q, ~R \lor ~Q, R \vdash ~P \]
| \( P \) | \( Q \) | * \( R \) | \( ~Q \) | \( ~R \) | * \( P \implies Q \) | * \( ~R \lor ~Q \) | * \( ~P \) |
|---|---|---|---|---|---|---|---|
| \( V \) | \( V \) | \( V \) | \( F \) | \( V \) | \( V \) | \( F \) | \( F \) |
| \( V \) | \( V \) | \( F \) | \( F \) | \( F \) | \( V \) | \( F \) | \( F \) |
| \( V \) | \( F \) | \( V \) | \( V \) | \( V \) | \( F \) | \( V \) | \( F \) |
| \( V \) | \( F \) | \( F \) | \( V \) | \( F \) | \( F \) | \( V \) | \( F \) |
| \( F \) | \( V \) | * \( V \) | \( F \) | \( V \) | * \( V \) | * \( V \) | * \( V \) |
| \( F \) | \( V \) | \( F \) | \( F \) | \( F \) | \( V \) | \( V \) | \( V \) |
| \( F \) | \( F \) | * \( V \) | \( V \) | \( V \) | * \( V \) | * \( V \) | * \( V \) |
| \( F \) | \( F \) | \( F \) | \( V \) | \( F \) | \( V \) | \( V \) | \( V \) |
As células marcadas com "*" destacam as hipóteses e a conclusão do argumento, bem como as linhas em que as hipótese são simultaneamente verdadeiras e o respectivo valor da conclusão.
Exemplo
Se o Vasco cair pra série \( B \), então seu treinador será demitido. Se seu treinador for demitido, então o astro do time, Dinamite, também sairá. Se Dinamite sair, então não mais torcerei pelo Vasco. Continuo sendo torcedor do Vasco. Logo, Dinamite não saiu do time e vasco não caiu para série B.
Simbolicamente, temos
\[ P \implies Q, Q \implies R, R \implies S, ~S \vDash ~R \land P \]
| \( P \) | \( Q \) | \( R \) | \( S \) | * \( P \implies Q \) | * \( Q \implies R \) | * \( R \implies S \) | * \( ~S \) | \( ~R \) | \( ~P \) | * \( ~R \land ~P \) |
|---|---|---|---|---|---|---|---|---|---|---|
| \( V \) | \( V \) | \( V \) | \( V \) | \( V \) | \( V \) | \( V \) | \( F \) | \( F \) | \( F \) | \( F \) |
| \( V \) | \( V \) | \( V \) | \( F \) | \( V \) | \( V \) | \( F \) | \( V \) | \( F \) | \( F \) | \( F \) |
| \( V \) | \( V \) | \( F \) | \( V \) | \( V \) | \( F \) | \( V \) | \( F \) | \( V \) | \( F \) | \( F \) |
| \( V \) | \( V \) | \( F \) | \( F \) | \( V \) | \( F \) | \( V \) | \( V \) | \( V \) | \( F \) | \( F \) |
| \( V \) | \( F \) | \( V \) | \( V \) | \( F \) | \( V \) | \( V \) | \( F \) | \( F \) | \( F \) | \( F \) |
| \( V \) | \( F \) | \( V \) | \( F \) | \( F \) | \( V \) | \( F \) | \( V \) | \( F \) | \( F \) | \( F \) |
| \( V \) | \( F \) | \( F \) | \( V \) | \( F \) | \( V \) | \( V \) | \( F \) | \( V \) | \( F \) | \( F \) |
| \( V \) | \( F \) | \( F \) | \( F \) | \( F \) | \( V \) | \( V \) | \( V \) | \( V \) | \( F \) | \( F \) |
| \( F \) | \( V \) | \( V \) | \( V \) | \( V \) | \( V \) | \( V \) | \( F \) | \( F \) | \( V \) | \( F \) |
| \( F \) | \( V \) | \( V \) | \( F \) | \( V \) | \( V \) | \( F \) | \( V \) | \( F \) | \( V \) | \( F \) |
| \( F \) | \( V \) | \( F \) | \( V \) | \( V \) | \( F \) | \( V \) | \( F \) | \( V \) | \( V \) | \( V \) |
| \( F \) | \( V \) | \( F \) | \( F \) | \( V \) | \( F \) | \( V \) | \( V \) | \( V \) | \( V \) | \( V \) |
| \( F \) | \( F \) | \( V \) | \( V \) | \( V \) | \( V \) | \( V \) | \( F \) | \( F \) | \( V \) | \( F \) |
| \( F \) | \( F \) | \( V \) | \( F \) | \( V \) | \( V \) | \( F \) | \( V \) | \( F \) | \( V \) | \( F \) |
| \( F \) | \( F \) | \( F \) | \( V \) | \( V \) | \( V \) | \( V \) | \( F \) | \( V \) | \( V \) | \( V \) |
| \( F \) | \( F \) | \( F \) | \( F \) | * \( V \) | * \( V \) | * \( V \) | \( V \) | \( V \) | \( V \) | * \( V \) |
Exemplo
Ou matemática é difícil ou os alunos não gostam de matemática. Se o português é fácil, então a matemática é facil. Os alunos gostam de matemática. Portanto, se matemática é difícil, então português é fácil.
Simbolicamente, temos
\[ A \underline{\lor} B, C \implies ~A, ~B \vDash A \implies C \]
| \( A \) | \( B \) | \( C \) | * \( A \underline{\lor} B \) | \( ~A \) | * \( C \implies ~A \) | * \( ~B \) | * \( A \implies C \) |
|---|---|---|---|---|---|---|---|
| \( V \) | \( V \) | \( V \) | \( F \) | \( F \) | \( F \) | \( F \) | \( V \) |
| \( V \) | \( V \) | \( F \) | \( F \) | \( F \) | \( V \) | \( F \) | \( F \) |
| \( V \) | \( F \) | \( V \) | \( V \) | \( F \) | \( F \) | \( V \) | \( V \) |
| \( V \) | \( F \) | \( F \) | * \( V \) | \( F \) | * \( V \) | * \( V \) | * \( F \) |
| \( F \) | \( V \) | \( V \) | \( V \) | \( V \) | \( V \) | \( F \) | \( V \) |
| \( F \) | \( V \) | \( F \) | \( V \) | \( V \) | \( V \) | \( F \) | \( V \) |
| \( F \) | \( F \) | \( V \) | \( F \) | \( V \) | \( V \) | \( V \) | \( V \) |
| \( F \) | \( F \) | \( F \) | \( F \) | \( V \) | \( V \) | \( V \) | \( V \) |
A tabela mostra que o argumento é inválido.
Exemplo
Se eu ganhar na megasena darei um carro a cada um de vocês. Eu não ganhei. Logo, vocês perderam os carros prometidos.
| \( P_{1} \) | \( P_{2} \) | * \( P_{1} \implies P_{2} \) | \( ~P_{1} \) | \( ~P_{2} \) |
|---|---|---|---|---|
| \( V \) | \( V \) | \( V \) | \( F \) | \( F \) |
| \( V \) | \( F \) | \( F \) | \( F \) | \( V \) |
| \( F \) | \( V \) | * \( V \) | * \( V \) | * \( F \) |
| \( F \) | \( F \) | \( V \) | \( V \) | \( V \) |
A tabela mostra que o argumento é inválido.
Regras de Inferência
O método de tabela-verdade pode ser exaustivo. Neste método, derivamos uma sequência de proposições a partir das hipóteses até atingir a conclusão. Aqui estão elas:
| Nome | Premissas | Conclusão |
|---|---|---|
| Simplificação | \( P \land Q \) | \( P \) |
| Adição | \( P \) | \( P \lor Q \) |
| Conjunção | \( P, Q \) | \( P \land Q \) |
| Silogismo Disjuntivo | \( P \lor Q, ~P \) | \( Q \) |
| Modus Ponens | \( P \implies Q, P \) | \( Q \) |
| Modus Tollens | \( P \implies Q, ~Q \) | \( ~P \) |
| Silogismo Hipotético | \( P \implies Q, Q \implies R \) | \( P \implies R \) |
| Absorção | \( P \implies Q \) | \( P \implies (P \land Q) \) |
| Dilema Construtivo | \( P \implies Q, R \implies S, P \lor R \) | \( Q \lor S \) |
| Dilema Destrutivo | \( P \implies Q, R \implies S, ~Q \lor ~S \) | \( ~P \lor ~R \) |
Exemplo
Passe o celular ou a carteira. Dou o relógio ou não dou o celular. Fico com os documentos ou não dou a carteira. Não fico com os documentos. Logo, dou o celular e o relógio. Em símbolos
\[ P \lor C, L \or ~P, N \lor ~C, ~N \vDash P \land L \]
(1) \( P \lor C \) Premissa
(2) \( L \lor ~P \) Premissa
(3) \( N \lor ~C \) Premissa
(4) \( ~N \) Premissa
(5) \( ~C \) (3, 4) Silogismo Disjuntivo
(6) \( P \) (1, 5) Silogismo Disjuntivo
(7) \( L \) (2, 6) Silogismo Disjuntivo
(8) \( P \land L \) (6, 7) Conjunção
Como chegamos na conclusão, temos que o argumento é válido.
Exemplo
Se não estudar, não serei aprovado. Se colar, não estudo. Se não perder a concentração, serei aprovado. Se desligo o celular, não perco a concentração. Logo, se colo, não desligo o celular. Em símbolos
\[ ~E \implies ~A, C \implies E, ~P \implies A, M \implies ~P \vDash C \implies ~M \]
(1) \( ~E \implies ~A \) Premissa
(2) \( C \implies ~E \) Premissa
(3) \( ~P \implies A \) Premissa
(4) \( M \implies ~P \) Premissa
(5) \( C \implies ~A \) (1, 2) Silogismo Hipotético
(6) \( ~A \implies P \) (3) Contrapositiva
(7) \( C \implies P \) (5, 6) Silogismo Hipotético
(8) \( P \implies ~M \) (4) Contrapositiva
(9) \( C \implies ~M \) (7, 8) Silogismo Hipotético
Árvore de Refutação
Involve provar que o arugmento não pode ser inválido. Assumimos a conclusão como falsa, e, se não encontrarmos nenhum argumento a favor, então o argumento é válido.
Uma conjunção gera somente um ramo, enquanto uma disjunção gera dois ramos.
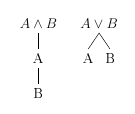
Se encontarmos uma contradição tipo \( P \) e \( ~P \) então o ramo é fechado.
Exemplo
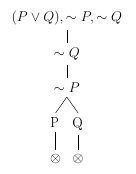
Verificar por meio de árvore de refutação a validade do argumento \( [(P \lor Q) \land ~P] \vDash Q \).
Exemplo
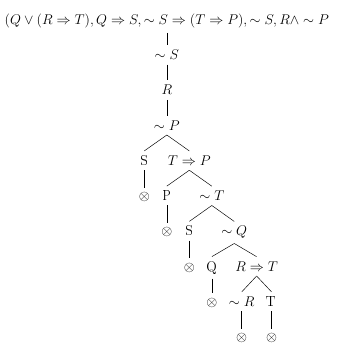
\[ (Q \lor (R \implies T), Q \implies S, ~S \implies (T \implies P), ~S \vDash R \implies P \]
Dica: simplificamos ao converter \( A \implies B \) em \( ~A \lor B \).
Exemplo
Considere o argumento \( {[P \implies (R \lor S)] \land [(R \land S) \implies Q]} \vDash (P \implies Q) \).

Como dois ramos ficaram abertos, o argumento é inválido.
Exemplo
Construa uma árvore de refutação para verificar se a fórmula \( (P \implies Q) \lor (P \land ~Q) \) é uma tautologia.

Argumentos Envolvendo Quantificadores
Regra 1: Dada qualquer função proposicional \( P(x) \), da verdade de \( \forall{x}, P(x) \), podemos inferir a verdade de \( P(a) \) para qualquer \( a \) no universo de discurso.
Regra 2: Dada qualquer função proposicional \( P(x) \), da verdade de \( \exists{x}, P(x) \), podemos inferir que existe pelo menos um elemento \( a \) no universo de discurso para o qual \( P(a) \) é verdadeiro.
Procure utilizar primeiro as proposições que envolvem quantificadores existenciais.
Exemplo
Prove a validade do seguinte argumento: "Todos os atletas são fisicamente fortes. Paulo é um atleta. Então Paulo é fisicamente forte."
Sejam \( A(x) : x \) é um atleta; \( F(x) : x \) é fisicamente forte. Assim,
(1) \( \forall{x}, A(x) \implies F(x) \) Premissa
(2) \( A(p) \) Premissa
(3) \( A(p) \implies F(p) \) Regra 1
(4) \( F(p) \) (2, 3) Modus Ponens
Exemplo
"Tudo é caro ou ruim para você. Nem tudo é ruim para você. Assim, existem algumas coisas que são caras e não são ruins para você."
Fazendo \( C(x) : x \) é caro e \( R(x) : x \) é ruim, obtemos:
(1) \( \forall{x}, [C(x) \lor R(x)] \) Premissa
(2) \( ~\forall{x}, R(x) \) Premissa
(3) \( \exists{x}, ~R(x) \) (2) Negação
(4) \( ~R(a) \) Regra 2
(5) \( C(a) \lor R(a) \) Regra 1
(6) \( C(a) \) (5, 4) Silogismo Disjuntivo
(7) \( C(a) \land ~R(a) \) (4, 6) Conjunção
(8) \( \exists{x}, [C(x) \land ~R(x)] \) Regra 2
Exemplo
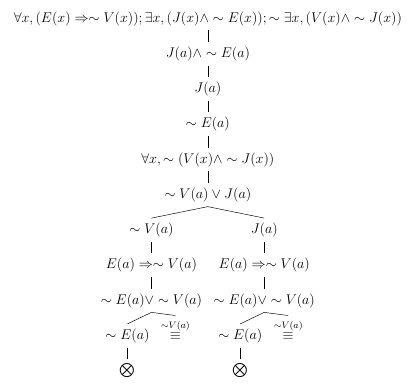
"Todos os cientistas são estudiosos. Alguns cientistas são inventores. Alguns estudiosos são inventores."
Faça \( C(x) : x \) é cientista; \( E(x) : x \) é estudioso; e \( I(x) : x \) é inventor. Tomando a negação da conclusão como hipótese adicional, obtemos que o argumento é válido, conforme a árvore de refutação abaixo:

Exemplo
Consideremos o seguinte arugmento: "Nenhum estudante é velho. Alguns jovens não são estudantes. Logo, alguns velhos não são jovens."
Faça \( E(x) : x \) é estudante; \( V(x) : x \) é velho; e \( J(x) : x \) é jovem. Então